razones trigonometricas

Para definir las razones trigonométricas de un ángulo cualquiera, se dibuja una circunferencia de radio 1. Los puntos sobre esta circunferencia tendrán por componente x el valor del coseno del ángulo y por componente y, el valor del seno del ángulo. Si se observa detenidamente, esta definición es equivalente para ángulos agudos a la definición de seno y coseno del apartado anterior, teniendo en cuenta que la hipotenusa mide 1, como puede observarse en este gráfico interactivo:

La tangente, y las razones trigonométricas restantes (secante, cosecante y cotangente), se definen a partir del seno y coseno. Debe tenerse en cuenta que existen ángulos para los que no es posible calcular alguna de estas razones trigonométricas porque en su expresión hay un cociente con denominador 0.

Para valores negativos o o para valores mayores de 2π$2\pi$ (en radianes, y 360º), se van repitiendo periódicamente sus razones trigonométricas, a partir de los de la primera circunferencia, tal como puede comprobarse:

Es decir, en radianes:

sen(α+2π)=sen(α−2π)=sen(α)$sen(\alpha +2\pi )=sen(\alpha -2\pi )=sen(\alpha )$
cos(α+2π)=cos(α−2π)=cos(α)$cos(\alpha +2\pi )=cos(\alpha -2\pi )=cos(\alpha )$

Además, para cualquier ángulo se sigue cumpliendo la igualdad básica de la trigonometría:

sen2x+cos2x=1$se{n}^{2}x+co{s}^{2}x=1$

Para acabar esta sección mira estos vídeos (también tienes la versión pdf):

versión pdf

Razones trigonométricas de los ángulos de 30º y 60º

Si cogemos un triángulo equilatero ABC, que como recordarás tiene todos sus lados (l) y sus ángulos iguales (60º), y lo dividimos por la mitad obtendremos dos triángulos rectángulos. 

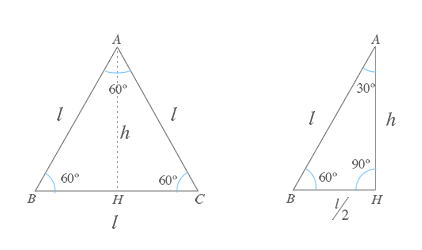
Descomposición de un triángulo equilatero
Al dividir por su altura un triángulo equilátero ABC como el de la figura obtendremos un triángulo rectángulo en el que los vértices A y B tendrán 30º y 60º respectivamente. 

Si conocemos el valor de los lados l, podemos calcular el valor de la altura por medio del teorema de pitágoras:

l2=h2+(l2)2;h=l2−(l2)2−−−−−−−−−√=34/⋅l2−−−−−−√=3–√2/⋅l

A partir de esta figura y aplicando la definición de seno, coseno y tangente de cualquier ángulo agudo podemos obtener las razones trigonométricas de los ángulos de 30º y 60º

Razones trigonométricas de los ángulos de 60º

Razones	Razones inversas
sin 60º=hl=cos 30º=3–√2	cosec 60º=lh= sec 30º = 23–√3
cos 60º=l2/l=sin 30º=12	sec 60º=ll2/=cosec 30º= 2
tg 60º=hl2/=cotg 30º=3–√	cotg 60º=l2/3√2/⋅l=tg 30º=3–√3

Razones trigonométricas de los ángulos de 30º

Razones	Razones inversas
sin 30º=l2/l=cos 60º=12	cosec 30º=ll2/=2
cos 30º=hl=sin 60º=3–√2	sec 30º=lh=23–√3
tg 30º=l2/h=cotg 60º=13–√=3–√3	cotg 30º=hl2/=3–√

Razones trigonométricas de los ángulos de 45º

Para determinar las razones trigonométricas de un ángulo de 45º tomaremos un cuadrado de lado l y lo dividiremos por su diagonal provocando que aparezcan dos triángulos isosceles. Recuerda que un triángulo isósceles tiene dos ángulos de 45º y uno de 90º.

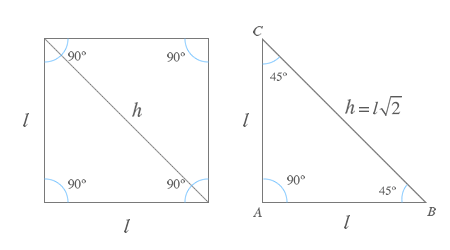
Descomposición de un cuadrado
Al dividir un cuadrado de lado l por su diagonal obtenemos dos triángulos isósceles cuya hipotenusa se puede obtener por medio del teorema de pitágoras.

h=l2+l2−−−−−√=l2–√

Razones trigonométricas de los ángulos de 45º

Si aplicamos las definiciones de las distintas razones trigonométricas sobre el anterior triángulo isósceles obtenemos que:

Razones	Razones inversas
sin 45º=lh=12–√=2–√2	cosec 45º=hl=2–√
cos 45º=lh=12–√=2–√2	sec 45º=2–√
tg 45º=ll=1	cotg 45º=ll=1

Razones trigonométricas de ángulos notables

	0º	30º	45º	60º	90º	180º	270º
sen	0	12	2–√2	3–√2	1	0	−1
cos	1	3–√2	2–√2	12	0	−1	0
tg	0	3–√3	1	3–√	∞	0	−∞
cosec	∞	2	22–√	23–√	1	∞	−1
sec	1	23–√	22–√	2	∞	−1	∞
cotg	∞	33–√	1	13–√	0	∞	0

Si observas la anterior tabla con atención puedes darte cuenta que para cualquier ángulo agudo se cumplen las siguientes ecuaciones:

sin α = cos(90º−α)

cos α = sin(90º−α)

tg α = cotg(90º−α)

Ejemplo

Conociendo las razones trigonométricas de 30º, 45º y 60º calcular las razones trigonométricas de los siguientes ángulos:

a) sen 1470º
b) cos 405º
c) tan 13π/3

Solución

Resolución

a) sen 1470º

Si tenemos en cuenta que el ángulo tiene más de 360º, podemos reducirlo al primer giro:

   1470º   360º       30º      4

Por lo tanto, 1470º es equivalente a 30º. Dado que conocemos el seno 30º:

sen 1470º = sen 30º =12

b) cos 405º

De igual forma que el apartado anterior podemos reducir el ángulo:

   405º   360º     45º   1

Teniendo en cuenta esto, se cumple que cos 405º = cos 45º. Conociendo el coseno de 45º:

cos 405º = cos 45º = 2–√2

c) tan 13π/3

En primer lugar vamos a convertir el ángulo en radianes a grados sexagesimales:

13π3rad=13π3⋅180ºπ=780º

Reduciendo los 780º al primer giro:

   780º   360º     60º    2

Teniendo en cuenta esto, se cumple que tan 780º = tan 60º. Conociendo la tangente de 60º:

tan 780º = tan 60º = 3–√